作者归档：runyu

机器学习笔记

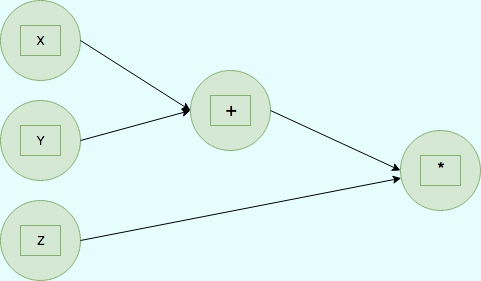
计算图是用图论语言表示数学函数的一种方式。计算图被定义为有向图，其中节点对应于数学运算。节点由边连接，图中的一切要么是节点，要么是边。

PyTorch提供的autograd包能够根据输入和前向传播过程自动构建计算图，并执行反向传播。

零阶张量：标量一阶张量：向量 Tensors of rank 1

线性回归

矩阵求导

范数 ∥x∥

前馈神经网络具有很强的拟合能力（通用近似定理）

正则化（Regularization）是一种在机器学习和统计学中广泛使用的技术，主要用于防止过拟合（Overfitting）。过拟合是指模型在训练数据上表现得很好，但在未见过的测试数据上表现较差。过拟合的原因通常是模型过于复杂，以至于它开始学习训练数据中的噪声，而非数据中真实的关系。

正则化通过向模型的损失函数（Loss function）添加一个额外的正则项（Regularization term）来实现。这个正则项通常与模型的权重（Weights）有关，可以帮助限制模型的复杂度。常见的正则化方法有L1正则化和L2正则化。

L1正则化将权重的绝对值之和添加到损失函数中，这会导致模型中的许多权重变为零，从而产生稀疏模型。L2正则化则将权重平方和添加到损失函数中，这会使得模型的权重更加接近于零，但不会产生稀疏解。

通过使用正则化，我们可以在模型复杂度和泛化能力之间找到一个平衡点，从而提高模型在未见过的数据上的性能。

归一化（Normalization）和正则化（Regularization）是两种不同的概念，它们在机器学习和统计学中都有重要的应用。以下是它们之间的主要区别：

目的：

归一化的目的是调整特征值的范围，以消除不同尺度和量纲对模型的影响。通过将特征值缩放到相同的范围（例如 [0, 1] 或者均值为 0，方差为 1 的正态分布），可以加快模型的收敛速度，提高模型的性能。

正则化的目的是防止模型过拟合，提高模型的泛化能力。通过在损失函数中添加正则项，正则化方法限制了模型权重的大小，从而降低了模型的复杂度。

方法：

归一化是一种预处理技术，通常在模型训练之前对数据进行处理。常见的归一化方法有最小-最大缩放（Min-Max Scaling）、Z分数标准化（Z-score Normalization）等。

正则化则是模型训练过程中使用的一种方法，通过向损失函数添加正则项来实现。常见的正则化方法有 L1 正则化和 L2 正则化。

总结一下，归一化主要关注数据预处理，使得特征值在相同的尺度上，以便于模型训练；而正则化关注模型的复杂度，通过限制模型权重的大小来防止过拟合。两者都对提高模型性能有积极作用，但它们的关注点和方法有所不同。

在机器学习模型中，尤其是神经网络模型中，权重（Weights）是指模型内部的参数，它们决定了模型如何根据输入特征来进行预测。模型权重的大小通常是指这些参数的数值大小。

以线性回归模型为例，模型的目标是学习一组权重 w 和偏置项 b，使得模型可以尽可能准确地预测输出 y。这个模型可以表示为：

y = w1 * x1 + w2 * x2 + … + wn * xn + b

其中，w1、w2、…、wn 是权重，x1、x2、…、xn 是输入特征，y 是预测输出，b 是偏置项。在这个例子中，权重的大小是指 w1、w2、…、wn 的数值大小。

在训练过程中，模型会调整权重和偏置项的值，以便在训练数据上获得最小的损失。权重的大小会影响模型的复杂度。权重较大可能导致模型过拟合，因为它可能会过度强调某些特征，从而在训练数据上表现得很好，但在新数据上泛化能力较差。而权重较小则会降低模型的复杂度，有助于防止过拟合，但是过小的权重可能导致模型欠拟合，即在训练数据和新数据上都表现不佳。

正则化方法（如 L1 和 L2 正则化）通过向损失函数添加一个与权重大小相关的正则项来限制权重的大小，从而在模型复杂度和泛化能力之间达到一个平衡。

梯度消失和模式崩溃是深度学习中常见的两种训练问题，尤其是在训练生成对抗网络（GAN）时。这两个问题的具体描述如下：

梯度消失（Gradient Vanishing）：梯度消失是指在训练深度神经网络时，网络中较低层的梯度值变得非常小，接近于零。这会导致权重更新变得非常缓慢，从而使网络难以学习到这些层的有用特征。梯度消失通常与激活函数（如 Sigmoid 和 Tanh）和深度网络结构有关。为了解决梯度消失问题，可以采用以下策略：
- 使用 ReLU（Rectified Linear Unit）或其他抗梯度消失的激活函数。
- 使用批量归一化（Batch Normalization）来减少梯度消失的影响。
- 使用残差连接（Residual Connection）以便梯度更容易地通过网络传播。
- 调整网络架构，减小网络深度。
模式崩溃（Mode Collapse）：模式崩溃是指在训练生成对抗网络（GAN）时，生成器产生的输出变得单一和相似，丧失了多样性。这通常是因为生成器和判别器之间的训练不平衡导致的。当生成器学会生成一种“简单”的输出以欺骗判别器时，它可能会陷入这种局部最优解。为了解决模式崩溃问题，可以采用以下策略：
- 为损失函数添加多样性惩罚项，以鼓励生成器产生更多样化的输出。
- 使用特征匹配（Feature Matching）或最小类间距（Minibatch Discrimination）等技术，以便判别器关注更丰富的特征。
- 调整训练策略，例如使用 WGAN（Wasserstein GAN）或 WGAN-GP（Wasserstein GAN with Gradient Penalty）等改进的 GAN 训练方法。
- 更平衡地训练生成器和判别器，例如使用 TTUR（Two Time-Scale Update Rule）。

这两个问题可能会影响模型的性能和训练速度，因此在训练深度学习模型和 GAN 时需要特别关注。解决这些问题通常需要调整网络架构、激活函数和训练策略等方面的设置。

为什么卷积网络可以接受不同尺寸的数据输入

卷积神经网络（Convolutional Neural Network，CNN）可以接受不同尺寸的数据输入，这是因为CNN中的卷积层和池化层等操作都是局部操作，不关心输入数据的整体尺寸大小，而是关注数据的局部结构和特征。

具体来说，卷积层通过滑动卷积核在输入数据上进行卷积操作，卷积核的大小是固定的，而输入数据的大小可以是任意的。卷积核在输入数据上滑动时，只关注当前滑动位置的局部区域，并进行卷积运算，因此输入数据的尺寸可以是任意的。

同样，池化层也是通过对局部区域进行池化操作，从而对数据进行下采样，进一步降低数据的尺寸大小。因此，池化层也可以接受不同尺寸的数据输入。

此外，卷积神经网络还可以通过使用全连接层等操作将输入数据的尺寸统一调整到相同的大小，以便于网络的后续处理。因此，卷积神经网络可以处理不同尺寸的输入数据，具有较强的灵活性和适应性。

卷积计算公式

W：输入特征图的宽，H：输入特征图的高

K：kernel size卷积核宽和高，P：padding（特征图需要填充的0的个数），S：stride步长

width_out：卷积后输出特征图的宽，height_out：卷积后输出特征图的高

普通卷积
计算公式：
width_out = （W – K + 2 * P）/ S + 1（向下取整）

height_out = （H – K + 2 * P） / S + 1（向下取整）

池化
计算公式：
width_out = （W – K）/ S + 1（向下取整）

height_out = （H – K） / S + 1（向下取整）

上采样UpSampling2D
上采样相当于放大多少倍，size=倍数

计算公式：
width_out = W * size

height_out = H * size

转置卷积
转置卷积俗称反卷积，是上采样方式中的一种，转置卷积用来增大特征图的分辨率。

计算公式：
width_out = （W – 1）* S – 2 * P + K

height_out = （H – 1）* S – 2 * P + K

nn.Upsample和nn.ConvTranspose2d都可以实现图像的上采样操作，但它们的具体实现方式有所不同。

nn.Upsample是一种常用的上采样方式，它通过对输入特征图进行插值操作来实现图像的放大。具体来说，nn.Upsample通过双线性插值等方式，对输入特征图中的每个像素进行放大，并生成相应大小的输出特征图。虽然nn.Upsample能够实现图像的上采样，但由于其采用了插值等方式，因此可能会产生一定程度的平滑或失真。

nn.ConvTranspose2d则采用卷积操作来实现图像的上采样。具体来说，nn.ConvTranspose2d会对输入特征图进行补零操作，并对补零后的特征图进行卷积操作。这样可以在保证特征图尺寸不变的同时，通过卷积操作实现图像的放大。与nn.Upsample相比，nn.ConvTranspose2d更加灵活，并且可以通过调整卷积核大小、步长、填充等参数来控制图像的清晰度和质量。

需要注意的是，nn.ConvTranspose2d可能会产生一些棋盘格等不良影响，而nn.Upsample不会产生这些问题。因此，实际应用中应该根据具体情况选择合适的上采样方式。

CycleGAN的原始生成器采用的是转置卷积，会产生棋盘格

消融实验

消融实验（ablation study）是指通过逐步削减模型中的某些模块或组件，来验证这些模块或组件对模型性能的贡献。它通常被用于探究模型中的某些设计选择的有效性和必要性，或者对某些假设进行验证。

具体来说，消融实验通常分为以下几个步骤：

定义基准模型：定义一个基准模型作为对照组，它是最基本的模型，包含所有的设计组件。基准模型通常具有较高的性能。
削减模型组件：逐步削减模型中的某些组件，比如某些层、某些特征、某些连接方式等，得到一系列消融模型。
测试消融模型：对所有的消融模型和基准模型进行测试，比较它们的性能差异。可以采用各种指标进行评估，比如准确率、F1-score等。
分析结果：根据测试结果，分析不同模型之间的性能差异。可以发现哪些模型组件对模型性能有重要的贡献，哪些模型组件对模型性能没有显著的影响。

通过消融实验，我们可以深入了解模型的性能和设计选择，从而为进一步的模型优化和改进提供指导。

卷积网络参数量计算
参数量 = (输入通道数 × 卷积核尺寸 × 卷积核尺寸 + 1) × 卷积核个数（输出通道数）

摘记

一个人的命运啊，当然要靠自我奋斗，但是也要考虑到历史的行程

Imagine life as a game in which you are juggling some five balls in the air. You name them — work, family, health, friends and spirit and you’re keeping all of these in the air.You will soon understand that work is a rubber ball.If you drop it, it will bounce back. But the other four balls — family, health, friends, and spirit — are made of glass. If you drop one of these, they will be irrevocably scuffed, marked, nicked, damaged, or even shattered. They will never be the same. You must understand that and strive for balance in your life.

Build your own things

神经网络

直观的理解：
Batch Size定义：一次训练所选取的样本数。
Batch Size的大小影响模型的优化程度和速度。同时其直接影响到GPU内存的使用情况，假如你GPU内存不大，该数值最好设置小一点。

为什么要提出Batch Size？
在没有使用Batch Size之前，这意味着网络在训练时，是一次把所有的数据（整个数据库）输入网络中，然后计算它们的梯度进行反向传播，由于在计算梯度时使用了整个数据库，所以计算得到的梯度方向更为准确。但在这情况下，计算得到不同梯度值差别巨大，难以使用一个全局的学习率，所以这时一般使用Rprop这种基于梯度符号的训练算法，单独进行梯度更新。
在小样本数的数据库中，不使用Batch Size是可行的，而且效果也很好。但是一旦是大型的数据库，一次性把所有数据输进网络，肯定会引起内存的爆炸。所以就提出Batch Size的概念。

Batch Size设置合适时的优点：
1、通过并行化提高内存的利用率。就是尽量让你的GPU满载运行，提高训练速度。
2、单个epoch的迭代次数减少了，参数的调整也慢了，假如要达到相同的识别精度，需要更多的epoch。
3、适当Batch Size使得梯度下降方向更加准确。

Batch Size从小到大的变化对网络影响
1、没有Batch Size，梯度准确，只适用于小样本数据库
2、Batch Size=1，梯度变来变去，非常不准确，网络很难收敛。
3、Batch Size增大，梯度变准确，
4、Batch Size增大，梯度已经非常准确，再增加Batch Size也没有用

注意：Batch Size增大了，要到达相同的准确度，必须要增大epoch。

Pytorch

class NeuralNetwork(nn.Module):
    def __init__(self):
        super(NeuralNetwork, self).__init__()
        self.flatten = nn.Flatten()
        self.linear_relu_stack = nn.Sequential(
                (28*28, 512),
            nn.ReLU(),
            nn.Linear(512, 512),
            nn.ReLU(),
            nn.Linear(512, 10),
            nn.ReLU()
        )
    def forward(self, x):
        x = self.flatten(x)
        logits = self.linear_relu_stack(x)
        return logits

在 PyTorch 中，对 tensor 执行 detach() 会返回一个新的 tensor，该 tensor 与原始 tensor 共享数据，但不会参与反向传播计算。具体来说：

共享数据：新 tensor 与原始 tensor 共享相同的数据，修改其中一个会影响另一个。
断开计算图：新 tensor 不会记录计算历史，因此不会在反向传播中计算梯度。
梯度计算：原始 tensor 的梯度计算不受影响，仍可正常进行。

示例代码

import torch

# 创建一个需要梯度的 tensor
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)

# 对 x 进行一些操作
y = x * 2

# 对 y 执行 detach
z = y.detach()

# 打印结果
print("y:", y)
print("z:", z)

# 进行反向传播
y.sum().backward()

# 打印 x 的梯度
print("x.grad:", x.grad)

输出

y: tensor([2., 4., 6.], grad_fn=<MulBackward0>)
z: tensor([2., 4., 6.])
x.grad: tensor([2., 2., 2.])

解释

y 是通过 x 计算得到的，保留了计算历史。
z 是 y 的 detach() 结果，与 y 共享数据但不参与反向传播。
反向传播后，x 的梯度正常计算，而 z 不影响梯度计算。

总结

detach() 用于从计算图中分离 tensor，常用于冻结部分模型参数或避免不必要的梯度计算。

如果只是对 GPU 上的 tensor 执行 .detach() 而不调用 .cpu()，那么 z 和 y 仍然会共享数据，因此对 z 的修改会反映到 y 上。

原因

.detach() 的作用：

返回一个新的 tensor，与原始 tensor 共享数据。
新 tensor 不会参与反向传播，但仍然与原始 tensor 共享底层存储。

共享数据：

如果 z 是通过 y.detach() 创建的，那么 z 和 y 共享相同的数据存储。
对 z 的修改会直接反映到 y 上，因为它们指向同一块内存。

验证代码

import torch

# 创建一个在 GPU 上的 tensor，并启用梯度计算
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True).cuda()

# 对 x 进行一些操作
y = x * 2

# 执行 .detach()，不调用 .cpu()
z = y.detach()

# 修改 z
z[0] = 100.0

# 打印 y 和 z
print("y:", y)  # y 的值被修改
print("z:", z)  # z 的值被修改

输出

y: tensor([100.,   4.,   6.], device='cuda:0', grad_fn=<MulBackward0>)
z: tensor([100.,   4.,   6.], device='cuda:0')

解释

y:
虽然 y 仍然在 GPU 上，并且保留了计算历史（grad_fn），但它的值被修改为 [100., 4., 6.]。
这是因为 z 和 y 共享数据。
z:
z 的值被修改为 [100., 4., 6.]。
由于 z 和 y 共享数据，y 的值也被同步修改。

总结

如果只调用 .detach()：
z 和 y 共享数据，对 z 的修改会反映到 y 上。
如果调用 .detach().cpu()：
z 会被移动到 CPU，并且与 y 不再共享数据，对 z 的修改不会影响 y。

因此，是否调用 .cpu() 是决定 z 和 y 是否共享数据的关键。

算法

大 O 表示法将始终假定算法将执行最大的迭代次数

完美二叉树, 完全二叉树和完满二叉树 – veli – 博客园 (cnblogs.com)

数学

最小二乘法（Least Squares Method）

线性回归（Linear Regression）

为什么有些时候，期望的符号是一个空心E？

空心E通常表示随机变量的期望，它也被称为数学期望、平均值或期望值。它表示对随机变量在其取值范围内所有可能取值的加权平均值。

与实心E表示样本的平均数不同，空心E表示的是随机变量的平均值。随机变量是指具有多个可能取值的变量，而这些值可能是离散的（例如投掷硬币的结果）或连续的（例如人的身高）。空心E可以用来计算随机变量的平均值，以便进行概率分析和推断。

魏尔施特拉斯逼近定理

魏尔斯特拉斯逼近定理有两个：

1.闭区间上的连续函数可用多项式级数一致逼近。

2.闭区间上周期为2π的连续函数可用三角函数级数一致逼近。

通用近似定理

对一个矩阵进行softmax操作的步骤如下：

计算每行的指数：对矩阵的每个元素计算指数。
按行求和：对每行的指数值求和。
归一化：将每个元素的指数值除以其所在行的指数和。

卷积神经网络

卷积神经网络（Convolutional Neural Network，CNN或ConvNet）是一种
具有局部连接、权重共享等特性的深层前馈神经网络．
卷积神经网络最早主要是用来处理图像信息．在用全连接前馈网络来处理
图像时，会存在以下两个问题：
（1）参数太多：如果输入图像大小为100 × 100 × 3（即图像高度为100，宽
度为 100 以及 RGB 3 个颜色通道），在全连接前馈网络中，第一个隐藏层的每个
神经元到输入层都有 100 × 100 × 3 = 30 000 个互相独立的连接，每个连接都对
应一个权重参数．随着隐藏层神经元数量的增多，参数的规模也会急剧增加．这
会导致整个神经网络的训练效率非常低，也很容易出现过拟合．
（2）局部不变性特征：自然图像中的物体都具有局部不变性特征，比如尺
度缩放、平移、旋转等操作不影响其语义信息．而全连接前馈网络很难提取这些
局部不变性特征，一般需要进行数据增强来提高性能．

池化<=>下采样